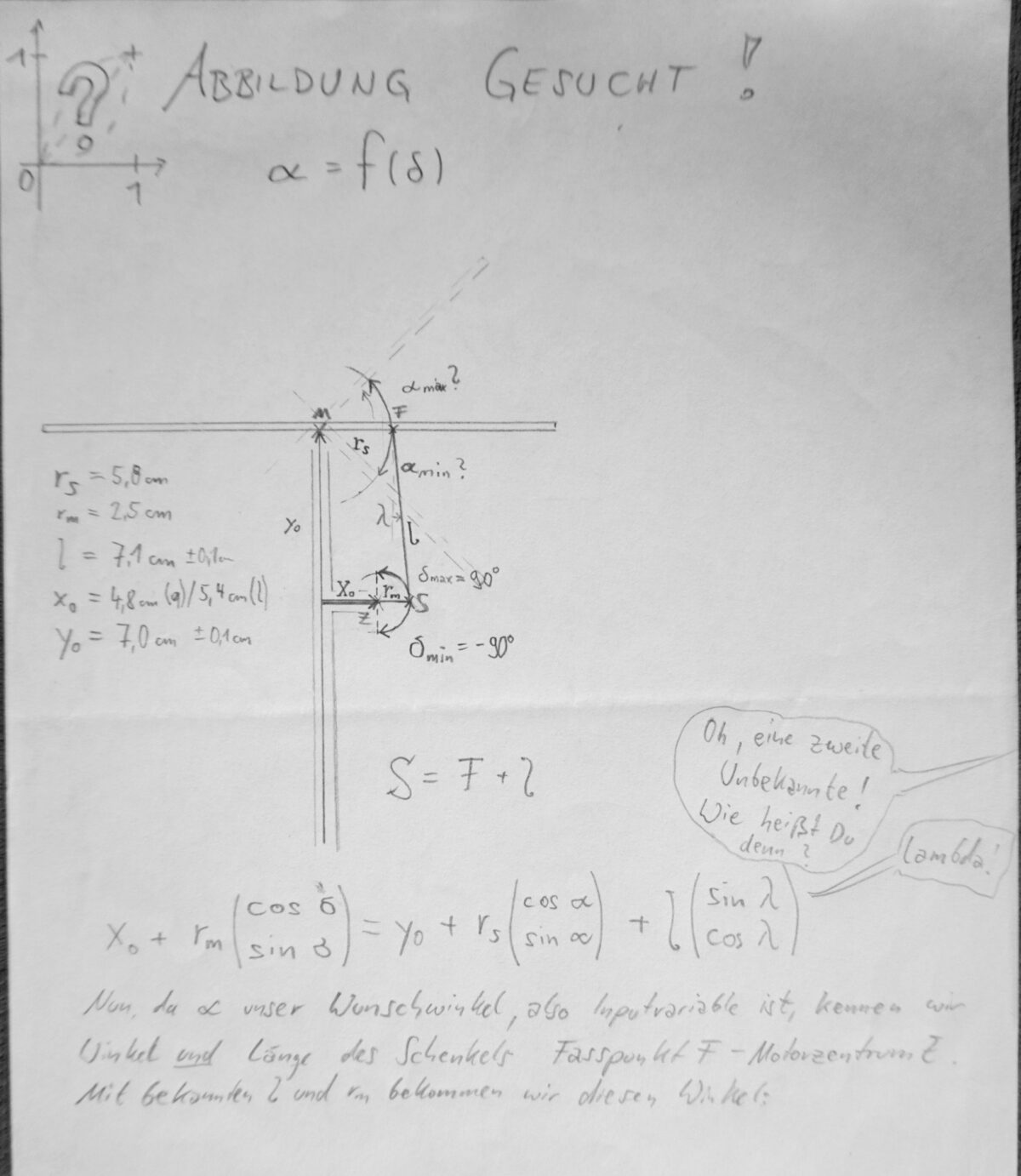
Die Spiegelelemente der Skulptur AURORA werden von Servomotoren bewegt, die 180° Bewegungsfreiheit haben. Die Arme an den Motoren sind aber nur 53mm lang, die Aufnahme an den Spiegeln ist dagegen 80mm vom Angelpunkt entfernt. Während die Motoren also ±90° drehen, neigen sie den Spiegel dabei nur etwa um ±45° je Achse. Bis jetzt wurden die Kalibrationspunkte einfach linear interpoliert, obwohl mit dieser Geometrie keine lineare Abbildung erfolgt.
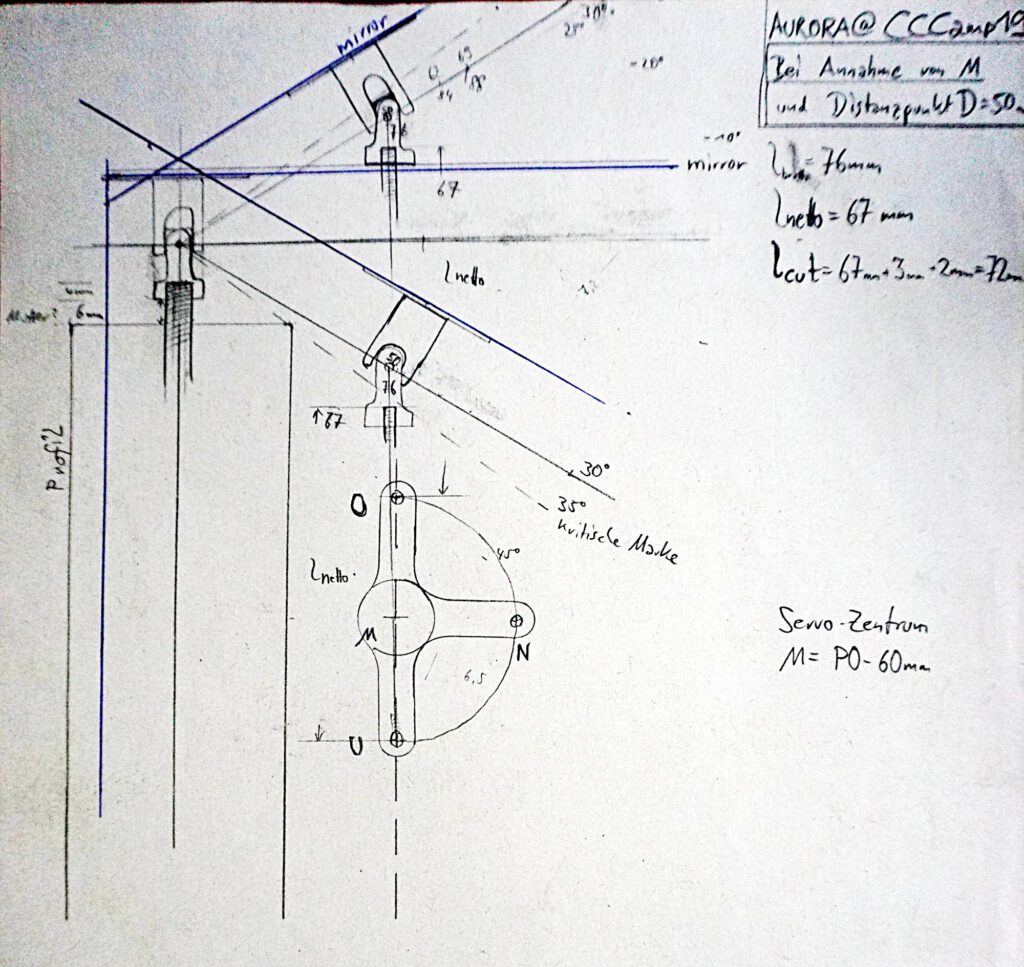
Formel gesucht
Schon vor einigen Jahren hatte ich das Problem einmal skizziert und eine erste Formel dazu.
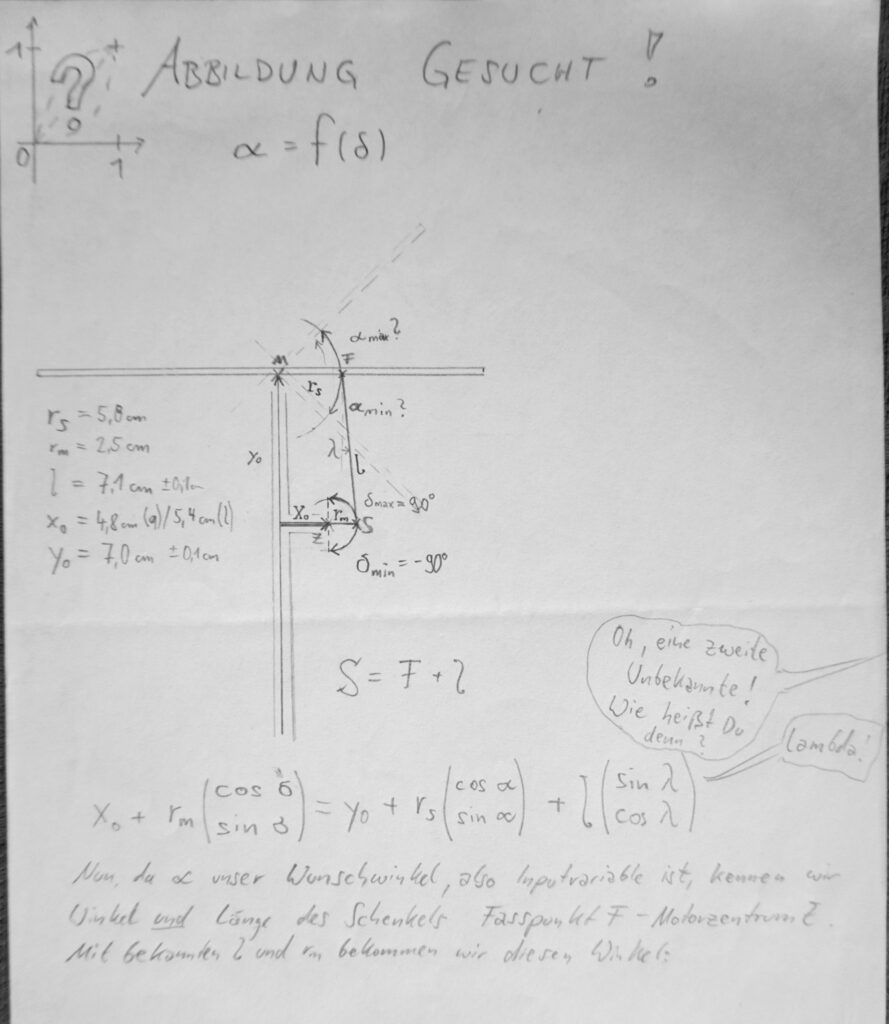
Erst jetzt bin ich dazu gekommen, diese endlich einmal nach dem gesuchten Motorwinkel aufzulösen und in Python korrekt zu plotten.
# Define the variables and function
Ms = glm.vec2(0,12.0) # Centers of the rotations.
Mm = glm.vec2(4.5,0) # Its German, so [m]otor and [s]piegel:
rm = 5.3 # Radius of circle m
rs = 8.0 # Radius of circle s
L = 12.0 # length of crank
# Calculation of alpha as a function of rho
def rho_from_alpha(alpha_deg, _L):
alpha = np.deg2rad(alpha_deg)
# coordinates of S on the mirror
Sx = Ms.x + rs * np.cos(alpha)
Sy = Ms.y + rs * np.sin(alpha)
# angle of the line Mm-S:
MmSx = Sx-Mm.x
MmSy = Sy-Mm.y
rho1 = np.arctan2(MmSx,MmSy)
# distance between motor axis and S on mirror
MmSls = MmSx**2+MmSy**2
MmSl = np.sqrt(MmSls)
# second component of the angle between vertical and crank
try:
rho2 = np.arccos((rm**2 + MmSls - _L**2) / (2*rm*MmSl))
except:
rho2 = np.nan
rho = np.pi/2 - rho1 - rho2
return rho
Witzigerweise bin ich auf der Suche nach besserer Formatierung der Gitterlinien in Matplotlib auf eine Seite gestoßen, die genau diese Aufgabe löst und auch noch den englischen Namen dafür benennt: Crank and Rocker Motion.
Da meine Implementation den genauen Punkt, wo das Motorhorn (Rocker) zu stehen kommt, nicht zeichnet, entfällt eine Berechnung, und dieser Punkt kann m.E. auch mit einem atan-Ausdruck weniger berechnet werden.
Jedenfalls steht aktuell aus,
- die Animation in der oben verlinkten Lösung in meiner Ausgabe als
subplotzu sehen, - diese beiden zu animieren und
- im Idealfall einige Parameter interaktiv zu machen.
Erkenntnisse über den Fußweg
Ich habe also zunächst einmal sehen wollen, wie sehr und wohin sich die Kurve bewegt, wenn z.B Unregelmäßigkeiten in der Länge des Kolbens (Crank) auftreten. Und siehe da:
Bei Abweichung um 2mm sieht man sofort, dass es ein Problem mit der Mittelstellung gibt, dass man entweder durch physische Korrektur oder durch weitere Geometriedaten per Motor lösen kann.
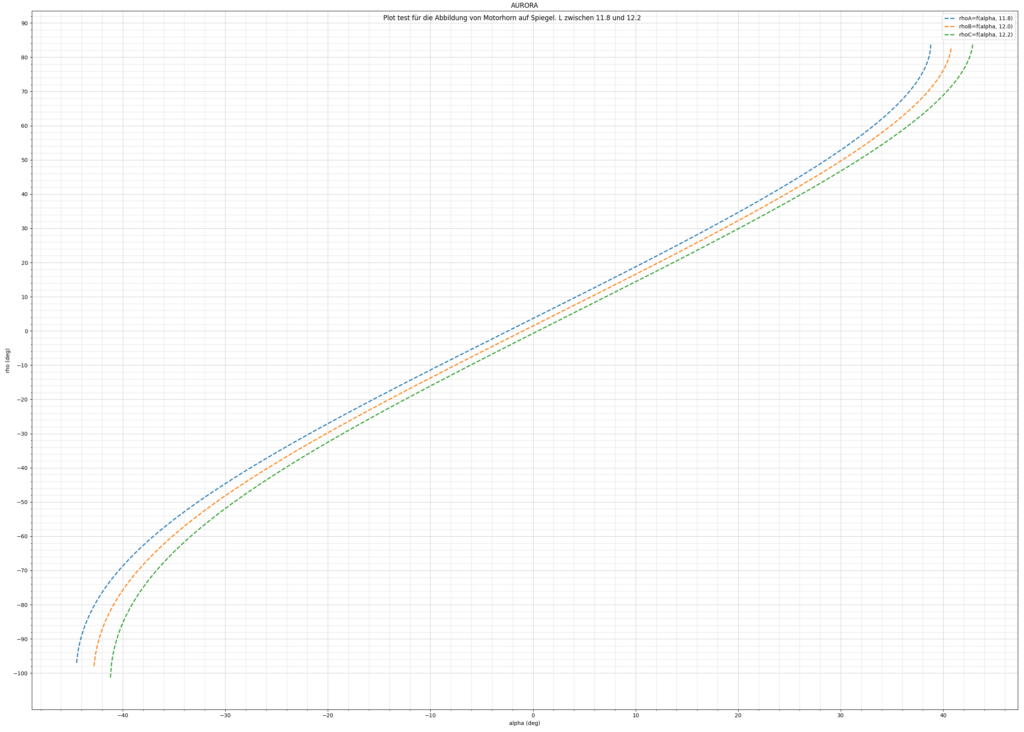
· während der Motor beim Einziehen unter -90° noch wirkt, ist beim Ausfahren bei 87° das Maximum erreicht. Geometrisch schlüssig.
· nur bei Kolbenlänge 12.2mm entspricht die Mittelposition des Motors auch der des Spiegels
· die Abbildung ist selbst zwischen ±30° nicht ausreichend linear,
· kann aber mit den richtigen Parametern über eine einfache Arkussinus-funktion super angenähert werden
Dazu interessiert mich nun, ob als physische Korrektur eine Verschiebung der Käfige mit je zwei Motoren die Abbildung wesentlich beeinflusst.
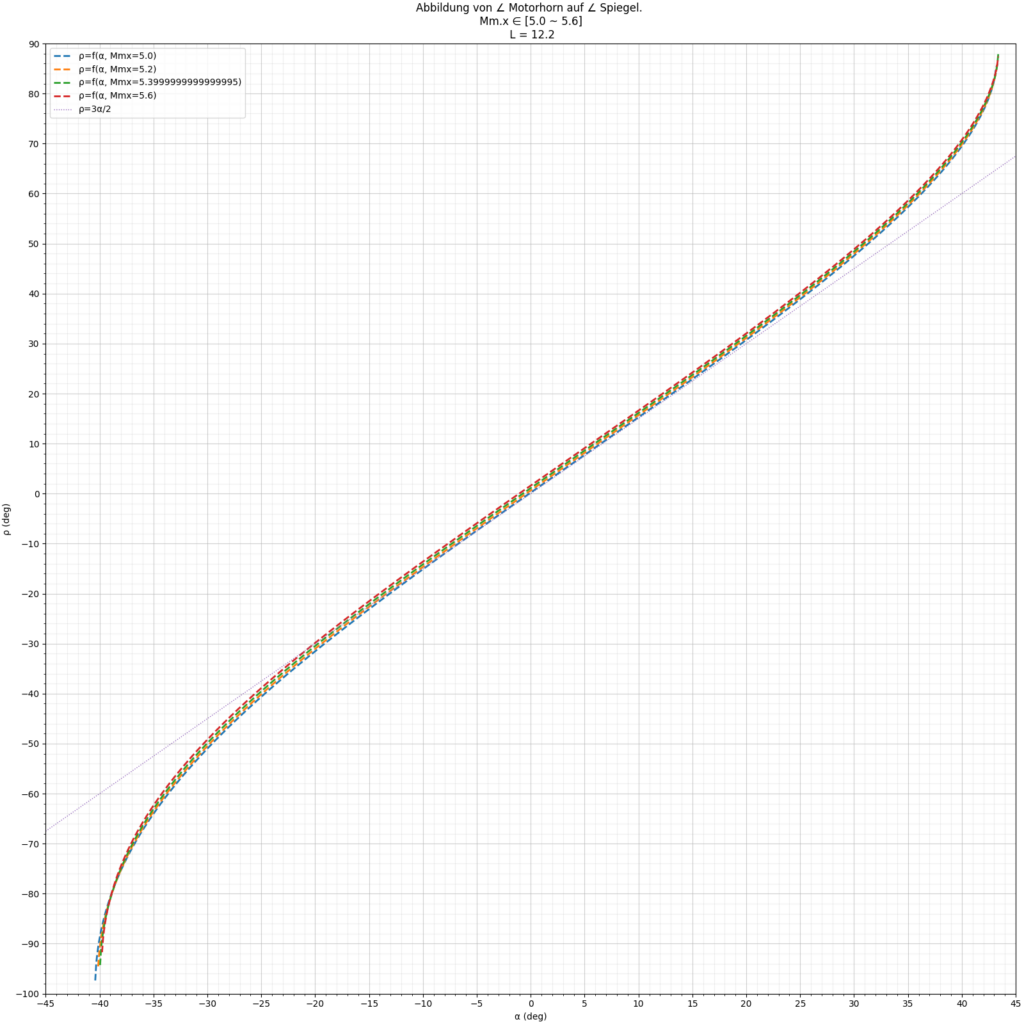
Abweichungen um ±2mm sind praktisch vernachlässigbar.
An dieser Stelle wird wurde es sinnvoll, die Variationen in dem Skript komfortabler zu handhaben, nämlich indem man die Kurvenschar in Schleifen errechnet und zeichnet statt jetzt dreimal manuell.
Approximation
Vermittels der Plots konnte ich wie angekündigt eine Annäherung vornehmen. Sie beinhaltet in ihrer linearen Komponente die Geometrie und ist für große positive Winkel nicht ideal:
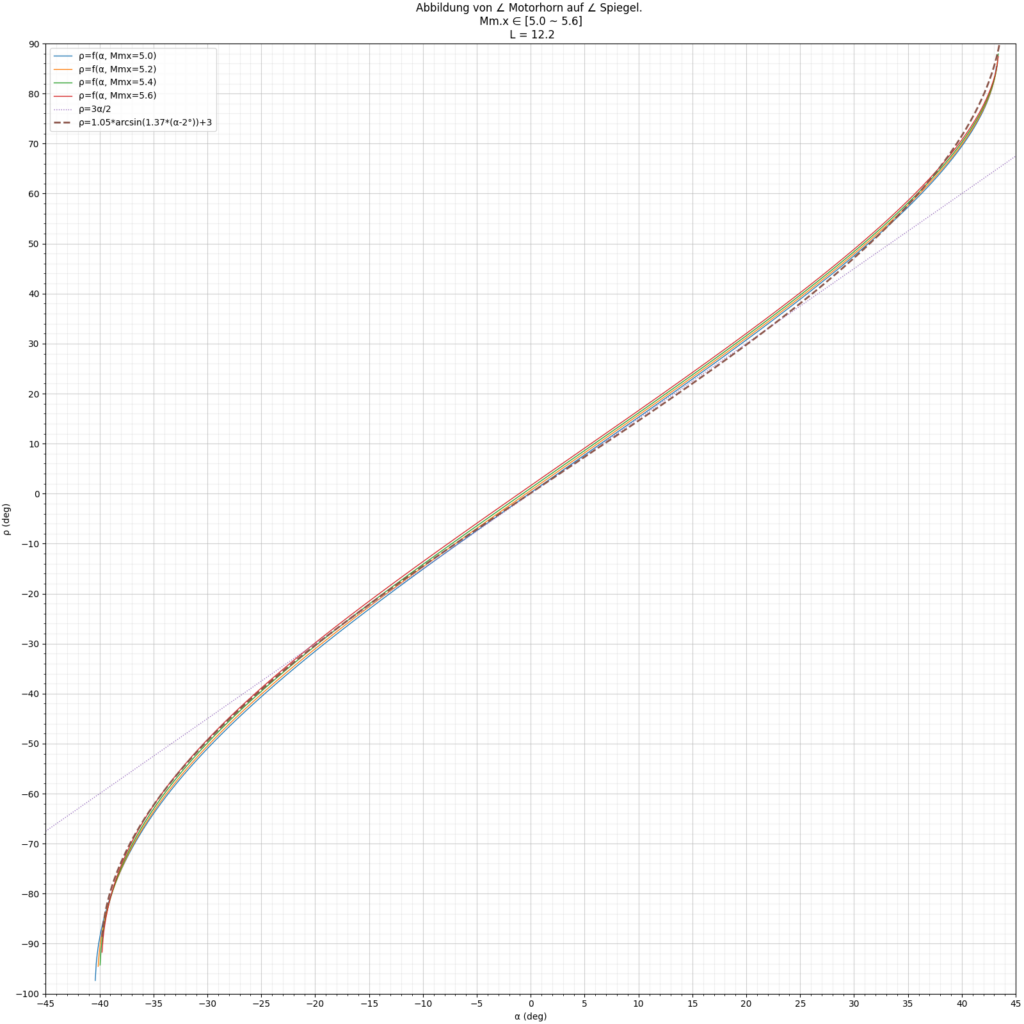
Insgesamt haben die Simulationen dieser Abbildung mittels Matplotlib ergeben:
- Die Käfige sollten so am Rahmen eingestellt werden, dass die Spiegel bei orthogonalem Motorhorn ebenfalls plan stehen. Das ist bei
L-2mmder Fall. Alle anderen Abweichungen sind vernachlässigbar. - Davon unberührt sind natürlich Abweichungen, die sich durch Kombination der beiden Auslenkungen ergeben. Ich erwarte einen leichten Kisseneffekt.
Darüberhinaus wird es schwierigere Fehlabbildungen geben durch Schwerkraft, von der insbesondere die vier seitlichen Dreiecke betroffen sind.
Bei neuerlichem Nachdenken wurde mir klar, dass die zuletzt genannten Abweichungen bei Kombination in 2D große Probleme darstellen. Wahrscheinlich muss eine völlig neue Formel für die Spiegelebene aus den drei Eckpunkten gefunden werden, denn die Achse der Drehung ändert sich ja beim Auslenken mit dem anderen Motor. In der Praxis sieht das ganz einfach und funktionierend aus, aber geometrtisch sind es mitnichten unabhängige Achsen zur Auslenkung in x bzw. y.